Fizik ve Matematik, doğa ve dil, insanoğlunun anlama çabası ve bu çaba için kullanılan araç.
Fiziğe aşığım. Çünkü Fizik yaşamıma anlam katıyor. Su ısıtıcısının düğmesine her bastığımda suyun elektrikle ısınması, duvardaki anahtara bastığımda odamın bir anda aydınlanması, köpeğime topu fırlattığımda onu düşmeden yakalaması, saatin tik tak larını duyduğumda zamanın geçtiğini hissetmem hatta o saatin içindeki mekanizmayı, suyun nasıl ısındığını bilmek topun havada nasıl süzüleceğini kestirebilmek…
 |
| Matematik doğa ile anlaşmamızı sağlayan bir dildir |
Başımıza nelerin geleceğini içgüdülerimizle kesin olmasa da önceden kestirebiliyoruz çünkü hepimiz doğuştan fizikçiyiz. Doğada hayatta kalabilmemiz, onunla iyi anlaşabilmemiz için fizikçi olmamız bir gereksinim. Peki ya doğaya hükmetmek onunla anlaşabilmek isteseydik. İşte o zaman doğayla konuşabilmemizi sağlayacak bir dil bulmamız gerekiyordu. Neyse ki bu dil önceden bulunmuş. İşte bu dile Matematik diyoruz. Matematik sayesinde ısıtıcının içindeki suyun kaç dereceye ne kadar sürede çıkacağını, ya da yerden bilmem kaç metre yükseklikteki aydınlatıcının odamın ne kadarlık bir alanını aydınlatacağını bir varsayıma gerek kalmadan net bir şekilde ifade edebiliriz. Fakat bazen matematiğin doğayı açıklamada yetersiz kaldığını düşündüğümüz anlar da olmuyor değil. Fizik ve matematikle aranız iyiyse ve çevrenizde de bu tarz kişiler çoksa size böyle bir soru gelebilir.
“Matematiksel olarak 0 ile 1 arasında sonsuz tane sayı olduğunu varsayarsak ve her şeyin bir yarımı olduğunu biliyorsak,uzunluk birimleri sonsuza kadar yarıma bölünebilir fakat fiziksel evrende en küçük birim Planck uzunluğudur ve her şey sonsuza kadar yarımına bölünemez. Bu konuda matematik fiziği anlamamız için yetersiz değil mi? ”
Bu soru bana çok sevdiğim bir arkadaşım tarafından soruldu üç gün önce. Ben de düşüncelerimi paylaşmak için böyle bir yazı yazma gereksinimi duydum.
Sorduğu soruyu Zenon Paradoksları'ndan Dikototomi Paradoksu'nu kullanarak açıklayabileceğimi düşündüm.
İlk olarak Dikototomi Paradoksunu açıklayayım.
Bir kişinin A noktasondan b noktasına gideceğini varsayalım.Fakat b’ye gitmeden, önce b’ye olan mesafenin yarısını gitmek zorundadır. Fakat b’ye olan mesafenin yarısını gitmeden önce bu mesafenin çeyreğini gitmesi gerektir. Daha sonra çeyreği gidebilmek için sekizde birini gitmesi gerekmektedir; bu böyle devam eder.
Sonuç olarak A kişisinin sonsuz sayıda mesafe gitmesi gerekir. Burada bir sorun daha vardır; her ilk mesafe aralığı ikiye bölünebileceği için gidilmesi gereken bir ilk mesafe yoktur. Böylece bu yolculuğun bir başlangıç noktası yoktur, yani yolculuğa başlayamaz. Bu paradoks sonuç olarak belirli bir mesafenin yolculuğunun tamamlanamaycağını veya başlanamayacağını, böylece de her hareketin sadece bir yanılsamadan ibaret olacağını ifade eder.
İşte matematiğin dünyasında biz sonsuza kadar gidilebilme ya da sonsuza kadar bölünebilme gibi kavramları çok rahat söyleyebildiğimizden bir çok paradoksa maruz kalıyoruz.Ama fiziksel dünyada işler böyle yürümüyor.
Mikroskobik dünyada bölme işlemi planck sabiti ölçeğine kadar yapılabilir. Zaten kuantum teorisi de bu ölçeğin altında bölme işleminin mümkün olamayacağını söylemektedir.Ancak bu yaklaşım mutlak bir sonuç olarak düşünülmemelidir. Zenon matematiksel soyut nesneler üzerinde çalıştığı için Zenon’un sonlu uzay bölgesinde bölme işlemi yapabilmek için fiziksel bir araca ihtiyacı yoktur. Ya da uzayın kuantize edilmiş olması gibi bir engelle karşılaşmaz. İşte matematiksel dünyada nesneler soyut olarak düşünüldüğü için bu işlem yapılabilir. Ama fiziksel dünyada işler bu şekilde yürümez. Nedeni ise fiziksel nesneleri bölmek için o nesneleri bölebileceğimiz araçlara ihtiyaç duyarız. Sonsuz bölme işlemini yapabilecek araçlar var olmadığı için zaten bu mümkün olamaz. Sadece araçlar değil kuantum teorisine göre nesnelerin kuantumlu yapısıda bu işlemi yapabilme ihtimalimizin önündeki en büyük engeldir. Matematik dünyasında bu tür engeller olmadığı için için Zenon paradoksunu çözmek amacıyla “uzay kuantize oldugu için sonsuz bölme işlemi yapılamaz “ya da “zenon paradoksuna bakarak uzayın sonsuza kadar bölünemeyeceği varsayımında bulunabiliriz” tarzı çıkarımlar yanlıştır. Matematik bir dildir ve soyuttur bu yüzden fiziksel dünyadaki somut nesnelerle bağdaştırılarak bu tarz çıkarımlarda bulunmak bir çelişki olduğunu göstermez.


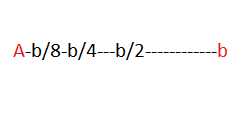







0 yorum:
Yorum Gönder